Let's go for a cliched beginning, shall we??
The Oxford Dictionary defines the noun "Aptitude" as "A natural ability to do something".
So what's the big deal with it right now, I hear you ask??
Well, with all things going well and by God's good grace, I'll be attending the second on-campus placement drive at the end of next month. Four years have passed since I've subjected myself to the rigours of aptitude tests. My attempt to test my aptitude at CAT last year was thwarted by the untimely arrival of Jaundice, which also played its part to put an end to my last career.
So, the oncoming tests and tribulations are, hopefully, the deliverance I've been waiting for since I can remember. Not to say that I'm studying my ass off or taking too much pressure from all this. In fact, the events of the just concluded week showed me up for being unprepared in many ways.
Aptitude. Again, that word makes it appearance. As an initial screening tool, most of the companies use Aptitude exams as a barometer to measure the capability of the interested applicants. Aptitude exams consists of mainly below tenth grade subject matter, derived from basic Mathematics, English and sense of logical reasoning. Of these, English is, thankfully, not that much of a problem for me (many thanks to this blog).
Logical reasoning for me is something which works superbly when it works, and fails miserably when it doesn't. And the other part is Mathematics. I've never failed to impress on anyone the undying love I've for the subject, with all its operators, x's, and integrals and transforms, etc etc. But I was stumped this week when I was asked what the root for a simple quadratic equation is.
That hurt the enormous amount of pride I had, and has resulted in some work on my part to brush up on the basics. And here, for the five things for this week, we'll go through some of the basic things in Mathematics.
***
1. Solving a general second degree polynomial equation.
Remember the variations of ax2 + bx + c = 0 we had to do to solve for x?? Well, at least remember the equation for the roots, the sum of roots and the product of roots. Very handy for such problems.
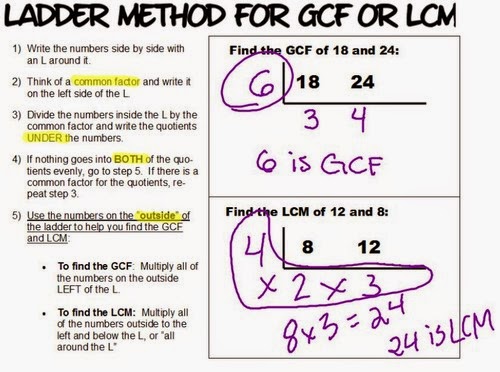
2. Finding the LCM and HCF of a set of numbers.
The quest for the Lowest Common Multiple and Highest(Greatest) Common Factor is made easier by the Ladder Method. It's explained below.
And here's another example
3. Area of a triangle from the length of the sides.
Heron's formula, often pun-ingly claimed and used as Hero's formula is what you use to get the answer for this problem. Explained nicely in the picture below.
4. The values of sin, cos and tan.
These values are very useful when you are trying to find the height of a tree on the other side of river. Remember the angles of incidence, elevation and depression??
5. BODMAS
I know, you'll claim this to be very simple. But do remember this when you do your calculations.
***
Even if you aren't preparing for an exam, I would advice you to go through such basic stuff once in a while. You surely wouldn't want to be in the position of the mother in the movie "1983", who had to escape from the scene when her child asks her what LCM is? :D ;)
***






No comments :
Post a Comment